Angular Strain Parameterization for Solving Static Cosserat Rods
Résumé
We show that static Cosserat rod clamped-free boundary value problems can be solved by only employing an angular strain parameterization. Consequently, the angular strain is discretized, while the linear strain remains continuous. This is made possible by leveraging the known boundary conditions at both ends of the rod and solving the balance equation of generalized moments. To assess this approach, our method is compared against the well-validated shooting and strain parameterization methods through two benchmarks. Compared to strain parameterization, our approach reduces the size of the residual vector, which considerably improves the computational time. Furthermore, since the linear strain is continuous, it converges more quickly to the solution, making shear and extension deformations more accurate. We have made our code available at https://gitlab.inria.fr/rjilani/ICRAX40.
Fichier principal
 ICRAX40_FI.pdf (507.42 Ko)
Télécharger le fichier
ICRAX40_FI.pdf (507.42 Ko)
Télécharger le fichier
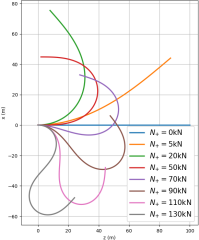 ICRAX40.png (63.51 Ko)
Télécharger le fichier
ICRAX40.png (63.51 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|---|
| Origine | Fichiers produits par l'(les) auteur(s) |


